|
Matlab toolbox for separation of convolutive mixtures |
|
| Toolbox main page | |
| How to use the toolbox | |
| Download | |
| Getting started | |
| Parameters/advanced usage | |
| Separation algorithm | |
| The deflation method | |
| Contrast functions | |
| References | |
Contrast functions
Note: for more informations on contrast functions (and particularly on quadratic contrast functions), see the references.
We give here is a brief description of the different contrast
functions proposed in the toolbox. We denote by ![]() the output of
the separating filter. When calling [Source,Contribution,W] =
Deflation(x,Param,FreqCycl);, the following contrast functions have
been implemented depending on the value of Param.Method:
the output of
the separating filter. When calling [Source,Contribution,W] =
Deflation(x,Param,FreqCycl);, the following contrast functions have
been implemented depending on the value of Param.Method:
- Case of stationnary sources:
- If Param.Method='kurtosisRealValued', the contrast:
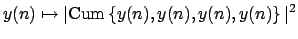
is maximized under the constraint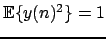 . This contrast
function is valid for real-valued stationnary sources.
. This contrast
function is valid for real-valued stationnary sources.
- If Param.Method='kurtosis', the contrast:
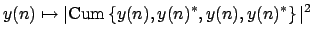
is maximized under the constraint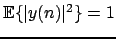 . This contrast
function is valid for both real-valued and complex-valued
stationnary sources.
. This contrast
function is valid for both real-valued and complex-valued
stationnary sources.
- If Param.Method='quadratic', the contrast:
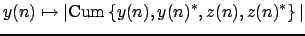
is maximized under the constraint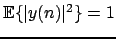 , where:
, where: 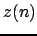 is a fixed ``reference'' signal. This contrast function is valid
for both real-valued and complex-valued stationnary sources. See
the references on quadratic contrasts for more information.
is a fixed ``reference'' signal. This contrast function is valid
for both real-valued and complex-valued stationnary sources. See
the references on quadratic contrasts for more information.
- If Param.Method='kurtosisRealValued', the contrast:
- Case of cyclo-stationnary sources: If
Param.Method='cyclostat', then the contrast:
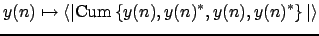
is maximized under the constraint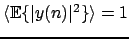 (where (
(where (
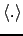 is the time average operator). This contrast function is valid for
both real-valued and complex-valued sources which are cyclo-stationnary.
is the time average operator). This contrast function is valid for
both real-valued and complex-valued sources which are cyclo-stationnary.



