|
Matlab toolbox for separation of convolutive mixtures |
|
| Toolbox main page | |
| How to use the toolbox | |
| Download | |
| Getting started | |
| Parameters/advanced usage | |
| Separation algorithm | |
| The deflation method | |
| Contrast functions | |
| References | |
The deflation method
We give a brief description of the deflation method implemented in the toolbox. Assume that the mixing model is the following one:
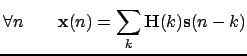 |
where:
-
-
-
The contrast functions implemented in the toolbox allow one to extract
one source from the mixture. After one source has been restored or if
a filtered version of one source has been extracted, one can subtract
its contribution in the observation signals. In so doing, the problem
of separating ![]() sources from the mixture simplifies to the problem
of separating
sources from the mixture simplifies to the problem
of separating ![]() sources. The so-called ``deflation'' method in
source separation is based on this idea. More precisely, the algorithm
(which has been implemented in Deflation.m) is the following
one:
sources. The so-called ``deflation'' method in
source separation is based on this idea. More precisely, the algorithm
(which has been implemented in Deflation.m) is the following
one:
- initialization:
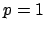 ; extraction of the first source
; extraction of the first source
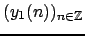 from the observations
from the observations
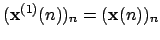 .
.
- for
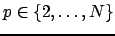 ,
,
- subtract the contribution of the source extracted at the
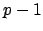 -th stage; this yields a signal
-th stage; this yields a signal
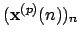 with
with
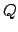 components but which corresponds to a reduced mixture of
components but which corresponds to a reduced mixture of
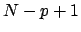 sources. (This is done in the program
SubtractSource.m).
sources. (This is done in the program
SubtractSource.m).
- extraction of a
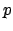 -th source
-th source
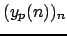 from the modified
observations
from the modified
observations
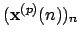 .
.
- subtract the contribution of the source extracted at the
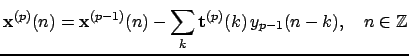 |
(1) |
where
| (2) |
In practice, the filters have finite impulse response and the above problem amounts to the least square solution of a linear system.
Note that deflation methods often lead to an accumulation of errors.



